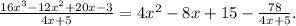Answer:
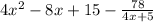
Explanation:
To solve polynomial long division problems like these, it's helpful to build a long division table. Getting used to building these can make problems like this much simpler to solve.
Begin by looking at the first term of the cubic polynomial.
What would we have to multiply
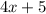 by to get an expression containing
by to get an expression containing
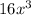 ? The answer is
? The answer is
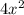 , since
, since
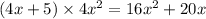 .
.
This is the first step of our long division, and we write out the start of our long division table like this:
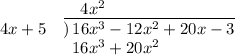
On the left is the divisor. On top is
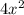 . In the middle is the polynomial we are dividing, and on the bottom is the result of multiplying our divisor by
. In the middle is the polynomial we are dividing, and on the bottom is the result of multiplying our divisor by
The next step is to subtract the bottom expression from the middle one, like so:
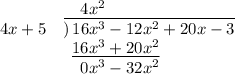
We are left with
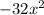 . The next thing to do is to add the next term of the polynomial we are dividing to the bottom line, like this:
. The next thing to do is to add the next term of the polynomial we are dividing to the bottom line, like this:
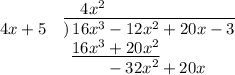
Now we return to the beginning of the instructions, and repeat the process: namely, what would we have to multiply
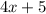 by to get an expression containing
by to get an expression containing
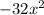 ? The answer is
? The answer is
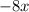 , and we fill out our long division table like so:
, and we fill out our long division table like so:
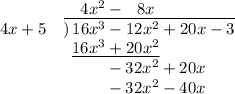
Once again, we subtract the bottom expression from the one above it, and include the next term of the divisor, like so:
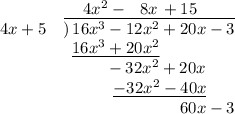
And repeat. What do we multiply
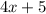 by to get an expression containing
by to get an expression containing
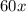 ? The answer is 15. Our completed long division table looks like this:
? The answer is 15. Our completed long division table looks like this:
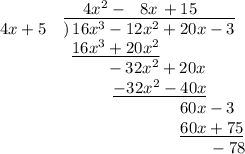
Now, the expression at the top,

is our quotient, and the last number,
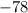 , is our remainder.
, is our remainder.
Hence we arrive at the solution of