Question

a railroad tracks can be determined using the following graph. Several different rosdways are in the same region as the railroad. Part B: A turnpikes route is determined by the equation y=1/3x^2. Prove algebraically how many intwrsections there will be between the railroad abd the turnpike,showing all necessary work

Answer 1

Given

`y=(1)/(3x^2)`

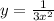
2x+3y=18

Find

Prove algebraically how many intwrsections there will be between the railroad

Step-by-step explanation

The graph of 2x+3y=18 is as the picture

2x+3y=18

when x=0, 0+3y=18 => y=6 =>(0,6)

when y=0, 2x+0=18 => x=9 => (9,0)

The intersection between the railroad and the highway is 0 because the graph of the railroad and the graph of the highway are parallel, that means they have no intersection

(b)

Assume the railroad can be found using the equation y=3/2x+b

when x=0 => y=8

`\begin{gathered} (1)/(3)x^2=(3)/(2)x+8 \\ 2x^2-9x-48=0 \\ D=9^2-4(2)(-48)=465 \\ =>D>0 \\ (1)/(3)x^2=(3)/(2)x+8 \end{gathered}`

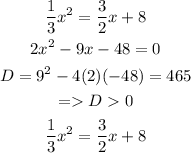
has two roots, and there are 2 intersections

Final Answer

(a) No intersection

(b) Two intersections