Remember that the average force F exerted over an object equals the change in the linear momentum of that object divided by the time over which the force is exerted:
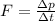
Assume that the direction towards Superman is negative and the direction away from Superman is positive. Find the initial and final linear momentum of General Zod, then calculate the change in the linear momentum and divide it by 1.5 seconds to find the average force exerted by Superman.
The linear momentum p of an object with mass m and speed v is given by:
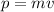
The mass of General Zod is 150kg. Its initial speed is 25 m/s towards Superman. Then, its initial velocity is negative and its initial linear momentum is:
![\begin{gathered} p_0=150\operatorname{kg}*-25(m)/(s) \\ =-3750\operatorname{kg}\cdot(m)/(s) \end{gathered}]()
The final speed of General Zod is 20 m/s away from Superman. Then, its final linear momentum is:
![\begin{gathered} p_f=150\operatorname{kg}*20(m)/(s) \\ =3000\operatorname{kg}\cdot(m)/(s) \end{gathered}]()
The change in the linear momentum of General Zod is:
![\begin{gathered} \Delta p=p_f-p_0_{} \\ =3000\operatorname{kg}\cdot(m)/(s)-(-3750kg\cdot(m)/(s)) \\ =3000\operatorname{kg}\cdot(m)/(s)+3750kg\cdot(m)/(s) \\ =6750\operatorname{kg}\cdot(m)/(s) \end{gathered}]()
Substitute Δp=6750 kg*m/s and Δt=1.5 s to find the force exerted by Superman:
![F=(\Delta p)/(\Delta t)=\frac{6750\operatorname{kg}\cdot(m)/(s)}{1.5s}=4500N]()
Therefore, the correct choice is option b) 4500 N.