Answer:
t₁ = 378.668 K
Step-by-step explanation:
From the given information:
The heat dissipated (q) from the electrical device =
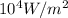
The contact resistance between device and aluminium;
(R_{const} ) = 0.5× 10⁻⁴ m² K/W
Conductivity of aluminum (k) = 238 \ W/mK
The thickness of aluminum plate (L) = 0.004 m
Convection coefficient (h) = 100 \ W/m^2 K
Surrounding temperature (t_2) = 278 \ k
According to Fourier's law of heat conduction.
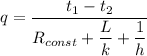
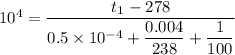
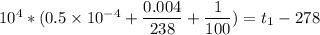

t₁ = 378.668 K