Answer:
∫
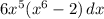 =
=
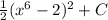
Explanation:
To find:
∫
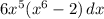
Solution:
Method of substitution:
Let
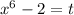
Differentiate both sides with respect to


[use
 ]
]
So,
∫
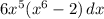 = ∫
= ∫
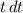 =
=
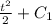 where
where
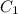 is a variable.
is a variable.
(Use ∫
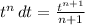 )
)
Put
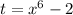
∫
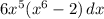 =
=
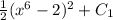
Use
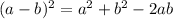
So,
∫
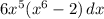 =
=

where
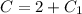
Without using substitution:
∫
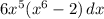 = ∫
= ∫
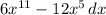 =
=
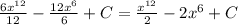
So, same answer is obtained in both the cases.