Question

WHAT THREE INEQUALITIES THAT DEFINES THE UNSHADED REGION

Answer 1

The three inequalities that define the unshaded region incude the following;

y ≤ -2x + 16

y > x + 5

x > 6

In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):

`y - y_1 = m(x - x_1)`

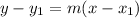
Where:

• x and y represent the data points.
• m represent the slope.

First of all, we would determine the slope for the downward slope solid line by using these points (8, 0) and (0, 16);

`Slope(m)=(y_2-y_1)/(x_2-x_1)`

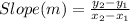
Slope (m) = (16 - 0)/(0 - 8)

Slope (m) = -2

At point (0, 16) and a slope of -2, an inequality for this line can be calculated by using the point-slope form as follows:

y - 16 = -2(x - 0)

y = -2x + 16

y ≤ -2x + 16 (since the solid line is shaded below).

At point (0, 5) and a slope of 1, an inequality for this line can be calculated by using the point-slope form as follows:

y - 5 = 1(x - 0)

y = x + 5

y > x + 5 (since the dashed line is shaded below).

Since the vertical solid line passes through the point (6, 0) and shaded above (to the right), an inequality that models it is given by;

x = 6

x > 6