Kindly check below
1) Let's do it in parts.
a) We can find the x-intercepts by using the factor zero property from each factor. Like this:
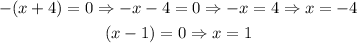
The best way to find the y-intercept with this factored form is by plugging into that equation x=0
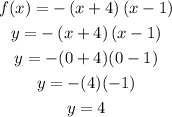
b) Expanding those factors by distributing them (FOIL) we can find this:

So now, let's find the x-coordinate of the vertex V(h,k):
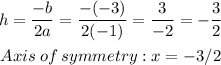
c) The coordinates of the vertex can be found by plugging the x-coordinate into the quadratic function. This way:
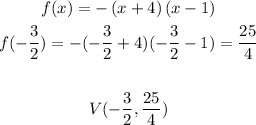
d) Finally, we can plot that function by setting a table:
So plotting these points (-2,6),(-1,6), (0,4), (1,0),(2,-6) and opening down the parabola for a is -1 we can plot this: