Question

A directed line segment begins at F(-8, -2), ends at H(8, 6), and is divided in the ratio 8 to 2 by G. What are the coordinates of G?

Answer 1

Given:

A directed line segment begins at F(-8, -2), ends at H(8, 6), and is divided in the ratio 8 to 2 by G.

To find:

The coordinates of point G.

Solution:

Section formula: If a point divide a line segment with end points
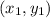`(x_1,y_1)` and
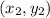`(x_2,y_2)` in m:n, then the coordinates of that point are

`Point=\left((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right)`

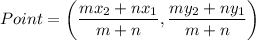
Point G divide the line segment FH in 8:2. Using section formula, we get

`G=\left((8(8)+2(-8))/(8+2),(8(6)+2(-2))/(8+2)\right)`

`G=\left((64-16)/(10),(48-4)/(10)\right)`

`G=\left((48)/(10),(44)/(10)\right)`

`G=\left(4.8,4.4\right)`

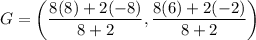
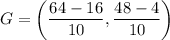
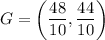
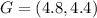
Therefore, the coordinates of point G are (4.8, 4.4).