This question is incomplete, the complete question is;
The owners of Spiffy Lube want to offer their customers a 10-minute guarantee on their standard oil change service. If the oil change takes longer than 10 minutes to complete, the customers is given a coupon for a free oil change at the next visit. Based on past history, the owners believe that the timer required to complete an oil change has a normal distribution with a mean of 8.6 minutes and a standard deviation of 1.2 minutes.
Suppose management could improve the process by reducing the mean time required for an oil change (but keeping the standard deviation the same). How much change in the mean service time would be required to allow for a 10-minute guarantee that gives a coupon to no more than 1 out of every 25 customers on average
Answer:
Required change in the mean service time is 7.8988
Explanation:
Given the data in the question;
How much change in the mean service time would be required to allow for a 10-minute guarantee that gives a coupon to no more than 1 out of every 25 customers on average
let mean = μ
p( x > 10 ) ≤ (1/25)
p( x > 10 ) ≤ 0.4
p( x-μ / 1.2 > 10-μ / 1.2 ) ≤ 0.4
(10-μ / 1.2 ) ≤ 0.4
(10-μ / 1.2 ) ≥
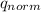 ( 0.96 )
( 0.96 )
(10-μ / 1.2 ≥ 1.751
10-μ = ≥ 1.751 × 1.2
10-μ ≤ 2.1012
μ ≤ 10 - 2.1012
μ ≤ 7.8988
Therefore, required change in the mean service time is 7.8988