Question

Please can i have help with part c

Answer 1

`\textsf{(a)}\quad \textsf{See below for proof.}`

`\textsf{(b)} \quad (x-7)^2+(y-5)^2=20`

`\textsf{(c)}\quad k = -19`

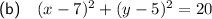
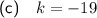
Explanation:

Given:

• The circle C has centre A with coordinates (7, 5).
• The line l, with equation y = 2x + 1, is the tangent to C at the point P.

`\hrulefill`

Part (a)

Line PA is the radius of circle C.

Since the tangent of a circle is perpendicular to its radius, then the slope of line PA is equal to the negative reciprocal of the slope of line l.

As the slope of line l is 2, then the slope of line PA is m = -1/2.

To find the equation of line PA, we can substitute the slope m = -1/2 and the coordinates of point A (7, 5) into the point-slope form of a linear equation:

`\begin{aligned}y-y_1&=m(x-x_1)\\\\y-5&=-(1)/(2)(x-7)\\\\2y-10&=-(x-7)\\\\2y-10&=-x+7\\\\2y+x&=7+10\\\\2y+x&=17\end{aligned}`

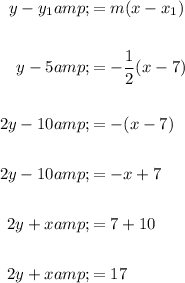
Hence, we have proved that the equation of the line PA is:

`\large\boxed{\boxed{ 2y + x = 17}}`

`\hrulefill`

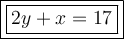
Part (b)

To find the equation for circle C, we first need to find the coordinates of point P.

Point P is the point of intersection of line l and line PA. Therefore, to find the x-coordinate of point P, substitute the equation of line l into the equation of line PA and solve for x:

`\begin{aligned}2(2x + 1)+x&=17\\\\4x+2+x&=17\\\\5x&=15\\\\x&=3\end{aligned}`

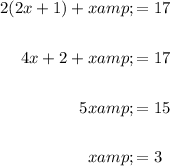
To find the corresponding y-coordinate of point P, substitute x = 3 into the equation for line l:

`\begin{aligned}y &= 2(3) + 1\\\\y &= 6 + 1\\\\y &= 7\end{aligned}`

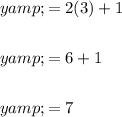
Therefore, the coordinates of point P are (3, 7).

The general equation of a circle with centre (h, k) and radius (r) is:

`(x-h)^2+(y-h)^2=r^2`

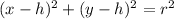
To find r², substitute the centre (7, 5) and point P (3, 7) into the general equation of a circle:

`\begin{aligned}(x-h)^2+(y-h)^2&=r^2\\\\(3-7)^2+(7-5)^2&=r^2\\\\(-4)^2+(2)^2&=r^2\\\\16+4&=r^2\\\\20&=r^2\\\\\end{aligned}`

Therefore, to write the equation of circle C, we can substitute the centre (7, 5) and r² = 20 into the general equation of a circle:

`\large\boxed{\boxed{(x-7)^2+(y-5)^2=20}}`

`\hrulefill`

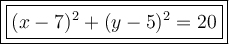
Part (c)

The line with equation y = 2x + k, k ≠ 1 is also a tangent to C.

To find the value of the constant k, we first need to find the other point where line PA intersects circle C, since the tangent to circle C at this point will have the same slope as line l.

To find the y-coordinates of the points of intersection of line PA and circle C, rearrange the equation for line PA so that x is the subject, then substitute this into the equation for circle C.

`\begin{aligned}\textsf{Line\;$PA$:}\quad 2y+x&=17\\\\x&=17-2y\end{aligned}`

Substitute this into the equation for circle C and solve for y:

`\begin{aligned}(x-7)^2+(y-5)^2&=20\\\\(17-2y-7)^2+(y-5)^2&=20\\\\(10-2y)^2+(y-5)^2&=20\\\\100-40y+4y^2+y^2-10y+25&=20\\\\5y^2-50y+125&=20\\\\5y^2-50y+105&=0\\\\y^2-10y+21&=0\\\\(y-3)(y-7)&=0\\\\\implies y&=3\\\implies y&=7\end{aligned}`

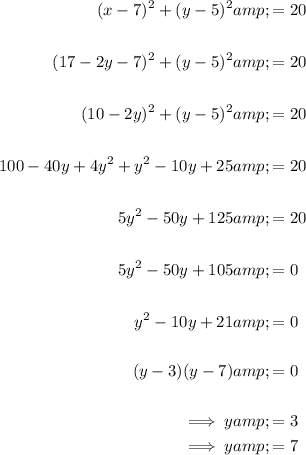
Therefore, the y-coordinates of the two points of intersection of line PA and circle C are y = 3 and y = 7.

As the y-coordinate of point P is y = 7, then the y-coordinate of the other point of intersection must be y = 3.

To find the corresponding x-coordinate of this point, we can substitute y = 3 into the equation for line PA:

`\begin{aligned}2(3) + x &= 17\\6+ x &= 17\\x&=11\end{aligned}`

Therefore, the other point of intersection of line AP and circle C is (11, 3).

Given the line with equation y = 2x + k is also a tangent to C, to find the value of the constant k, simply substitute point (11, 3) into y = 2x + k:

`\begin{aligned}3 &= 2(11) + k\\3 &= 22 + k\\k&=-19\end{aligned}`

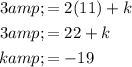
Therefore, the value of the constant k is:

`\large\boxed{\boxed{k = -19}}`