Question

A growth-mindset researcher plans to take an SRS of 200 teenagers from the population of teenagers in North America to see what proportion of teenagers sampled are pursuing a goal they have set for themselves. Suppose that 75% of teenagers in North America are pursuing a goal they have set for themselves. Let p represent the proportion of a sample of 200 teenagers in North America who are pursuing a goal they have set for themselves. What are the mean and standard deviation of the sampling distribution of p?

Answer 1

The mean of the sampling distribution of p is 0.75 and the standard deviation is 0.0306.

Explanation:

Central Limit Theorem:

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
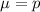`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

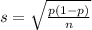
75% of teenagers in North America are pursuing a goal they have set for themselves.

This means that
`p = 0.75`

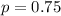
Sample of 200.

This means that
`n = 200`.

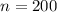What are the mean and standard deviation of the sampling distribution of p?

By the Central Limit Theorem

Mean
`\mu = p = 0.75`

Standard deviation
`s = \sqrt{(0.75*0.25)/(200)} = 0.0306`

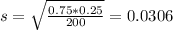
The mean of the sampling distribution of p is 0.75 and the standard deviation is 0.0306.