Question

Q 19.23: A proton is initially moving at 3.0 x 105 m/s. It moves 3.5 m in the direction of a uniform electric field of magnitude 120 N/C. What is the kinetic energy of the proton at the end of the motion

Answer 1

The kinetic energy of the proton at the end of the motion is 1.425 x 10⁻¹⁶ J.

Step-by-step explanation:

Given;

initial velocity of proton,
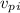`v_p_i` = 3 x 10⁵ m/s

distance moved by the proton, d = 3.5 m

electric field strength, E = 120 N/C

The kinetic energy of the proton at the end of the motion is calculated as follows.

Consider work-energy theorem;

W = ΔK.E

`W =K.E_f - K.E_i`

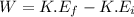
where;

K.Ef is the final kinetic energy

W is work done in moving the proton = F x d = (EQ) x d = EQd

`K.E_f =EQd + (1)/(2)m_pv_p_i^2`

`m_p \ is \ mass \ of \ proton = 1.673 \ * \ 10^(-27) kg \\\\Q \ is \ charge \ of \ proton = 1.6 * 10^(-19) C`

`K.E_f = 120* 1.6 * 10^(-19) * 3.5 \ + \ (1)/(2)(1.673* 10^(-27))(3* 10^5)^2 \\\\`

`K.E_f = 6.72* 10^(-17) \ + \ 7.53 * 10^(-17) \\\\K.E_f = 14.25 * 10^(-17) J\\\\K.E_f = 1.425* 10^(-16) \ J`

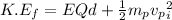
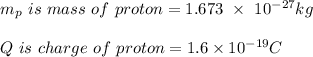
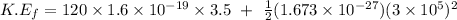
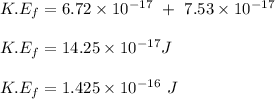
Therefore, the kinetic energy of the proton at the end of the motion is 1.425 x 10⁻¹⁶ J.