Question

A string of density 0.01 kg/m is stretched with a tension of 5N and fixed at both ends. The length of the string is 0.1m. What is the first four resonance frequencies in the string?

Answer 1

The first four resonance frequency in the string are;

1) 50·√50 Hz

2) 100·√50 Hz

3)150·√50 Hz

4) 200·√50 Hz

Step-by-step explanation:

The given parameters of the string are;

The density of the string, ρ = 0.01 kg/m

The tension force on the string, T = 5 N

The length of the string, l = 0.1 m

Therefore the mass of the string, m = Length of string × Density of the string

∴ m = 0.01 kg/m × 0.1 m = 0.001 kg

The formula for the fundamental frequency, f₁, is given as follows;

`f_1 = \frac{\sqrt{(T)/(m/L) } }{2 \cdot L} = \frac{\sqrt{(T)/(\rho) } }{2 \cdot L}`

Where;

f₁ = The fundamental frequency in the string

T = The tension in the string = 5 N

m = The mass of the string = 0.001 kg

L = The length of the string = 0.1 m

ρ = The density of the string = 0.01 kg/m

By plugging in the values of the variables, we have;

`f_1 = \frac{\sqrt{(5)/(0.01) } }{2 * 0.1} = 50 \cdot √(5)`

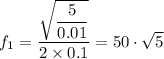
The first four harmonics are;

f₁, 2·f₁, 3·f₁, 4·f₁

Therefore, we have the first four resonance frequency of the string are as follows;

1 × 50·√50 Hz = 50·√50 Hz

2 × 50·√50 Hz = 100·√50 Hz

3 × 50·√50 Hz = 150·√50 Hz

4 × 50·√50 Hz = 200·√50 Hz