Question

Suppose that the manufacturer of a gas clothes dryer has found that, when the unit price is p dollars, the revenue R (in dollars) is R(P) = -9p2 + 18,000p. What unitprice should be established for the dryer to maximize revenue? What is the maximum revenue?

Answer 1

Suppose that the manufacturer of a gas clothes dryer has found that, when the unit price is p dollars, the revenue R (in dollars) is R(P) = -9p2 + 18,000p. What unit

price should be established for the dryer to maximize revenue? What is the maximum revenue?

we have the quadratic equation

`R(p)=-9p^2+18,000p`

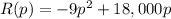
this is a vertical parabola, open downward

the vertex represents a maximum

Convert to factored form

Complete the square

factor -9

`R(p)=-9(p^2-2,000p)`
`R(p)=-9(p^2-2,000p+1,000^2-1,000^2^{})`
`\begin{gathered} R(p)=-9(p^2-2,000p+1,000^2)+9,000,000 \\ R(p)=-9(p^{}-1,000)^2+9,000,000 \end{gathered}`

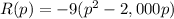
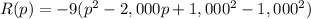
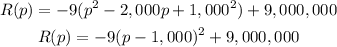
the vertex is the point (1,000, 9,000,000)

therefore

the price is $1,000 and the maximum revenue is $9,000,000

Problem N 2

we have the equation

`C(x)=0.7x^2+26x-292+(2800)/(x)`

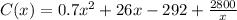
using a graphing tool

the minimum is the point (8.58,308.95)

therefore

Part a

the average cost is minimized when approximately 9 lawnmowers ........

Part b

the minimum average cost is approximately $309 per mower