Question

The Crews family went on a day trip to Nashville. For lunch they paid $7.50 for each adult meal and $5 for each child meal for a total of $65. For dinner the family paid $10.50 for each adult meal and $5 for each child meal for a total of $77. How many adults and how many children were on the trip?

Answer 1

Number of adult were on the trip = 4

Number of child were on the trip = 7

Explanation:

Let the Number of adult were on the trip = x

Let the Number of child were on the trip = y

As given,

For lunch they paid $7.50 for each adult meal and $5 for each child meal for a total of $65.

⇒7.50x + 5y = 65 ...........(1)

Also,

For dinner the family paid $10.50 for each adult meal and $5 for each child meal for a total of $77.

⇒10.50x + 5y = 77 ...........(2)

Now,

Subtract equation (2) from equation (1) , we get

10.50x + 5y - ( 7.50x + 5y ) = 77 - 65

⇒10.50x + 5y - 7.50x - 5y = 12

⇒10.50x - 7.50x = 12

⇒3x = 12

⇒x =
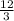`(12)/(3)` = 4

⇒x = 4

Now,

Put the value of x in equation (2) , we get

10.50(4) + 5y = 77

⇒42 + 5y = 77

⇒5y = 77 - 42

⇒5y = 35

⇒y =
`(35)/(5)` = 7

⇒y = 7

∴ we get

Number of adult were on the trip = x = 4

Number of child were on the trip = y = 7