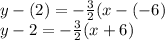Answer (assuming the equation can be written in point-slope form):
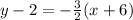
Step-by-step explanation:
When knowing a point the line crosses through and its slope, you can write an equation in point-slope form, or
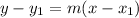 .
.
1) First, find the slope of the line. Use the slope formula
 and the x and y values of the two points given, then solve like so:
and the x and y values of the two points given, then solve like so:
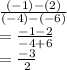
Thus, the slope is
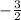 .
.
2) Now, use point-slope form,
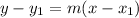 . Substitute the
. Substitute the
 ,
,
 , and
, and
 for real values.
for real values.
The
 represents the slope, so substitute
represents the slope, so substitute
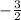 in its place. The
in its place. The
 and
and
 represent the x and y values of one point the line crosses through. Any of the two points will work, and I chose (-6,2) for this answer. So, substitute -6 for
represent the x and y values of one point the line crosses through. Any of the two points will work, and I chose (-6,2) for this answer. So, substitute -6 for