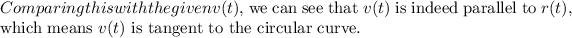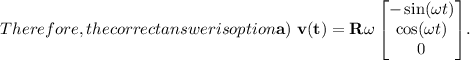Final Answer:
The correct velocity function is
 =
=
 . It is tangent to the circular curve, signifying the car's motion without external force would cause it to leave the curve.
. It is tangent to the circular curve, signifying the car's motion without external force would cause it to leave the curve.
Step-by-step explanation:
Let's analyze the given velocity function and determine whether it is tangent to the circular curve.
The velocity function provided is
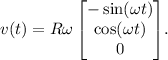
Here,
 represents the radius of the circular curve
represents the radius of the circular curve
 is the angular velocity, and
is the angular velocity, and
 is time.
is time.
To show that
 is tangent to the circular curve, we need to find the position vector
is tangent to the circular curve, we need to find the position vector
 of a point on the curve and then take the derivative of
of a point on the curve and then take the derivative of
 to obtain the velocity vector
to obtain the velocity vector
 . If
. If
 is parallel to
is parallel to
 , it indicates that
, it indicates that
 is tangent to the curve.
is tangent to the curve.
Assuming the circular curve is in the xy-plane, the position vector can be expressed as
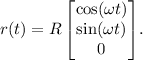
Now, let's find the derivative of
 with respect to
with respect to
 to obtain the velocity vector:
to obtain the velocity vector:
![\[ (dr)/(dt) = R\omega \begin{bmatrix} -\sin(\omega t) \\ \cos(\omega t) \\ 0 \end{bmatrix} \].](https://img.qammunity.org/2024/formulas/physics/high-school/phvo31o7p73rh5flfm15qfurwvareyyxs9.png)