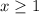We want to calculate the following quotient
![\frac{\sqrt[]{28(x-1)}}{\sqrt[]{8x^2}}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/7lqlmjx9k0i70at13kcn.png)
Note that using properties of radicals, given non zero numbers a,b we have that
![\frac{\sqrt[]{a}}{\sqrt[]{b}}=\sqrt[]{(a)/(b)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/jq9uzruc9nulf16x1vfa.png)
So, using this fact, our quotient becomes
![\sqrt[]{(28(x-1))/(8x^2)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/udth4rw9wnub0wm9bdsv.png)
As we are taking the square root, this opearation is only valid if and only if the expression inside the square root is a non negative number. That is, we must have that
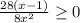
As this is a quotient, we should also that the quotient is defined.
To understand this last point, we should make sure that we are not dividing by 0. So first, we want to exclude those value s of 0 for which the denominator becomes 0. So we have the following auxiliary equation
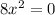
which implies that x=0.
So, the second quotient is always defined whenever x is different from 0. However, assuming that x is not 0 we want to find the value of x for which
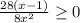
To start with this problem, we solve first the equality. So we have
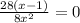
since x is not 0, we can multiply both sides by 8x², so we get
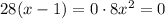
If we divide both sides by 28, we have that
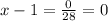
now, by adding 1 on both sides we get that
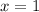
so, whenever x=1, we have that the quotient inside the radical becomes 0.
Now, we will solve the inequality, that is
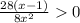
Note that on the left, we are mostly dividing two expressions. Recall that the quotient of two expressions is positive if and only if both expressions have the same sign.
Note that the expression
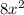
is the product of number 8 (which is positive) with the expression x², which is also always positive for any value of x. This means that the expression 8x² is always positive.
So, taking this into account, we should focus on those values of x for which the numerator is positive, as the denominator is always positive. So we end up with the following inequality
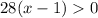
If we divide both sides by 28 we get
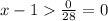
So, if we add 1 on both sides, we get
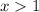
So, whenever x is greater than 1, the expression inside the radical is positive.
This means that the original quotient is defined whenever x=1 and whenever x>1. Thus, we would have