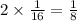Answer:
Foci
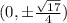
Vertices:
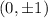
Eccentricity, e=
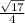
Length of latus rectum=
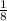
Explanation:
We are given that
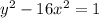

The equation of hyperbola is along y-axis because y is positive
Compare the equation with
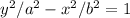 (Along y-axis)
(Along y-axis)
We get
a=1, b=1/4

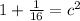
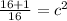
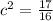
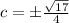
Therefore,
The coordinates of foci=
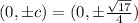
The coordinated of vertices=
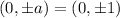
Eccentricity, e=c/a

Length of latus rectum=
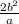
Length of latus rectum=