Question

6x-12=78 solve the 2 step equation and check the soultion ​

Answer 1

Answer: x is 15

Explanation:

`{ \tt{6x - 12 = 78}}`

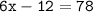
» Apply the addition rule of equality by adding 12 on either sides:

`{ \tt{(6x - 12) + { \green{12}} = 78 + { \green{12}}}} \\ { \tt{6x = 90}}`

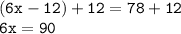
» Apply the division rule of equality by dividing either sides by 6

`{ \tt{ \frac{6x}{{ \blue{6}}} = \frac{90}{{ \blue{6}}} }} \\ \\ { \tt{x = (90)/(6) }} \\ \\ { \underline{ \tt{ \: \: x = 15 \: \: }}}`

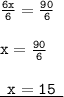
• Checking the solution :

`{ \tt{6x - 12 = 78}}`

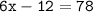
» Substitute x with its value (15) in the equation:

`{ \tt{6(15) - 12 = 78}} \\ { \tt{90 - 12 = 78}} \\ { \boxed{ \tt{ \: 78 = 78 \: }}}`

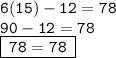
• Since the left hand side is equal to the right hand side, the value of x is consistent.