Question

After the end of an advertising campaign, the daily sales of a product fell rapidly, with daily sales given by S=3800e−0.05x dollars, where x is the number of days from the end of the campaign.a. What were daily sales when the campaign ended?b. How many days passed after the campaign ended before daily sales were below half of what they were at the end of the campaign?

Answer 1

Since the given equation is

`S=3800e^(-0.05x)`

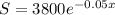
S is the amount of the daily sales from ending to x days

Since the form of the exponential function is

`y=ae^x`

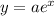
Where a is the initial amount (value y at x = 0)

Then 3800 represents the daily sales when x = 0

Since x = 0 at the ending of the campaign, then

a. The daily sales when the campaign ended is $3800

Since the daily sales will be below half $3800 after x days

Then find half 3800, then equate S by it, then find x

`\begin{gathered} S=(1)/(2)(3800) \\ S=1900 \end{gathered}`
`1900=3800e^(-0.05x)`

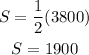
Divide both sides by 3800

`\begin{gathered} (1900)/(3800)=(3800)/(3800)e^(-0.05x) \\ (1)/(2)=e^(-0.05x) \end{gathered}`

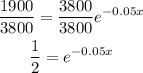
Insert ln for both sides

`\ln ((1)/(2))=\ln (e^(-0.05x))`

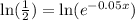
Use the rule

`\ln (e^n)=n`
`\ln ((1)/(2))=-0.05x`

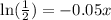
Divide both sides by -0.05 to find x

`\begin{gathered} (\ln ((1)/(2)))/(-0.05)=(-0.05x)/(-0.05) \\ 13.86294=x \end{gathered}`

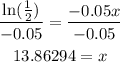
Since we need it below half 3800, then we round the number up to the nearest whole number

Then x = 14 days

b. 14 days will pass after the campaign ended