Question

In the triangular prism below, angle BDE = 23°. Calculate the volume of the prism. Give your answer in m³ to 1 d.p. ​

Answer 1

15820.1 m³

Explanation:

The volume of a triangular prism is equal to the product of the area of its triangular base and the length of the prism. So, in the case of the given triangular prism:

`\textsf{Volume} = \textsf{Area of $\triangle ABE$} * AD`

To find the area of triangle ABE, we first need to find the length of its legs, AB and BE.

Assuming that triangle BAD is a right triangle where m∠BAD = 90°, we can use Pythagoras Theorem to find the length of AB.

In ΔBAD, its hypotenuse is BD = 55 and its legs are AB and AD = 29. Therefore:

`AB^2+AD^2=BD^2`

`AB^2+29^2=55^2`

`AB^2=55^2-29^2`

`AB=√(55^2-29^2)`

`AB=√(2184)`

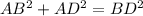
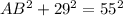
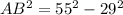
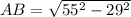
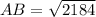
Assuming that triangle EBD is a right triangle where m∠EBD = 90°, and given that m∠BDE = 23° and BD = 55, we can use the tangent trigonometric ratio to find the exact length of BE:

`\tan \theta=\sf (Opposite\;side)/(Adjacent\;side)`

`\tan BDE=(BE)/(BD)`

`\tan 23^(\circ)=(BE)/(55)`

`BE=55\tan 23^(\circ)`

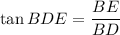
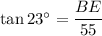
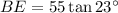
Now we have determined the exact lengths of AB and BE, we can create an equation to calculate the volume of the prism, remembering that the area of a right triangle is half the product of its legs:

`\textsf{Volume}=\left((1)/(2)* AB * BE\right) * AD`

`\textsf{Volume}=\left((1)/(2)* √(2184) * 55\tan 23^(\circ)\right) * 29`

`\textsf{Volume}=(55√(2184)\tan 23^(\circ))/(2) * 29`

`\textsf{Volume}=(1595√(2184)\tan 23^(\circ))/(2)`

`\textsf{Volume}=15820.0895...`

`\textsf{Volume}=15820.1\; \sf m^3\;(1\;d.p.)`

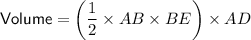
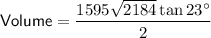
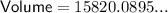
Therefore, the volume of the prism is 15820.1 m³, rounded to one decimal place.