Question

12^½/3^³/²


plsss help fast​

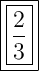
Answer 1

`(2)/(3)`

Explanation:

Given rational expression:

`(12^(\frac12))/(3^(\frac32))`

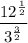
To evaluate the given rational expression, begin by rewriting 12 as the product of its prime factors:

`(\left(2^2 * 3\right)^(\frac12))/(3^(\frac32))`

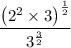
Now, apply the power of a product rule of exponents to the numerator:

`(\left(2^2\right)^(\frac12) * 3^(\frac12))/(3^(\frac32))`

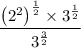
Apply the power of a power rule of exponents to
`\left(2^2\right)^(\frac12)`:

`(2^(2* \frac12) * 3^(\frac12))/(3^(\frac32))`

`(2^(\frac22) * 3^(\frac12))/(3^(\frac32))`

`(2^(1) * 3^(\frac12))/(3^(\frac32))`

`(2* 3^(\frac12))/(3^(\frac32))`

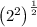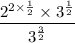
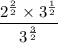
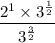
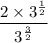
Rewrite the exponent in the denominator as the sum of 1 and 1/2:

`(2* 3^(\frac12))/(3^(1+\frac12))`

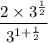
Apply the product rule of exponents to the exponent in the denominator:

`(2* 3^(\frac12))/(3^(1)* 3^(\frac12))`

`(2* 3^(\frac12))/(3* 3^(\frac12))`

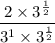
Cancel the common factor
`3^(\frac12)`:

`(2* \diagup\!\!\!\!\!3^(\frac12))/(3* \diagup\!\!\!\!\!3^(\frac12))`

`(2)/(3)`

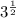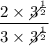
Therefore, the evaluation of the given rational expression is:

`\Large\boxed{\boxed{(2)/(3)}}`

`\hrulefill`

`\boxed{\begin{array}{rl}\underline{\sf Exponent\;Rules}\\\\\sf Power\;of\;a\;Product:&(ab)^m=a^mb^m\\\\\sf Power\;of\;a\;Power:&(a^m)^n=a^(mn)\\\\\sf Product:&a^m * a^n=a^(m+n)\\\\\end{array}}`