Question

a particle is projected with a velocity u=20ms^-1 at an angle 45°.The time after which it moves at an angle 15° with horizontal is ??? g=10ms^-2​

Answer 1

t ≈ 1.04 s

Step-by-step explanation:

To solve this problem, we'll analyze the motion of the particle projected at an angle and determine the time when its trajectory makes a 15° angle with the horizontal.

Given:

• v₀ = 20 m/s at 45°
• g = -10 m/s²

`\hrulefill`

First, let's break down the initial velocity into horizontal and vertical components.

Recall,

`\vec v_(x)=\vec v \cos(\theta)\\\\\vec v_(y)=\vec v \sin(\theta)`

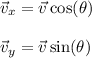
Finding the components, starting with the initial horizontal component:

`\Longrightarrow \vec v_(0_x)=\vec v_0 \cos(\theta)\\\\\\\\\Longrightarrow \vec v_(0_x)=(20 \ m/s) \cos(45 \textdegree)\\\\\\\\\therefore \vec v_(0_x) = 10 √(2) \ m/s`

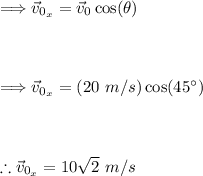
Now the initial vertical component:

`\Longrightarrow \vec v_(0_y)=\vec v_0 \sin(\theta)\\\\\\\\\Longrightarrow \vec v_(0_y)=(20 \ m/s) \sin(45 \textdegree)\\\\\\\\\therefore \vec v_(0_y) = 10 √(2) \ m/s`

Next, we consider the motion when the particle makes a 15° angle with the horizontal. At this moment, the velocity components will satisfy:

`\Longrightarrow \tan(15 \textdegree)=(\vec v_(f_y) )/(\vec v_(f_x))`

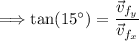
Here, 'v_x' remains constant throughout the flight because there's no horizontal acceleration. Plug in what we know to find 'v_fy':

`\Longrightarrow \tan(15 \textdegree)=(\vec v_(f_y) )/(10 √(2) \ m/s)\\\\\\\\\Longrightarrow \vec v_(f_y) =(10 √(2) \ m/s) \tan(15 \textdegree)\\\\\\\\\therefore \vec v_{y_(f)} \approx 3.789 \ m/s`

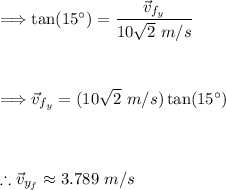
Thus, the vertical component of velocity is approximately 3.789 m/s when the particle makes a 15° angle with the horizontal. Now, using the following kinematic equation we can find the time:

`\Longrightarrow \vec v_(f_y)=\vec v_(0_y)+\vec a_y t\\\\\\\\\Longrightarrow t=(\vec v_(f_y)-\vec v_(0_y))/(\vec a_y)`

Plugging in our values:

`\Longrightarrow t=(3.789 \ m/s - 10 √(2) \ m/s)/(-10 \ m/s^2)\\\\\\\\\therefore t \approx \boxed{1.04 \ s}`

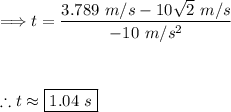
Thus, the time at which the particle is moving at a 15 degree angle is approximately 1.04 s.