Question

2. Calculate the mean, median and mode for the following data pertaining to marks in statistics. and verify mode graphically. Marks more than 0 20 40 60 80 100 120 Numbers of students 80 76 50 28 18 9 3​

Answer 1

a. The mean marks are approximately 29.92.

b. The median is 20.

c. The mode is 0 since it has the highest frequency of 80 students.

How to find the mean, median, and mode

To find the mean, median, and mode for the given data, let's start by organizing the data:

Marks: 0, 20, 40, 60, 80, 100, 120

Number of Students: 80, 76, 50, 28, 18, 9, 3

Mean:

The formula for the mean (average) is the sum of all values divided by the total number of values.

`\bar{x} = \frac {\sum fx}{\sum x}`

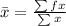
`\bar{x}` = (0 * 80 + 20 * 76 + 40 * 50 + 60 * 28 + 80 * 18 + 100 * 9 + 120 * 3) / (80 + 76 + 50 + 28 + 18 + 9 + 3)

Mean = (0 + 1520 + 2000 + 1680 + 1440 + 900 + 360) / 264

Mean = 7900 / 264

Mean ≈ 29.92

The mean marks are approximately 29.92.

Median:

The median is the middle value when the data is arranged in ascending order. If there's an even number of values, the median is the average of the two middle values.

To find the median:

Arrange the marks in ascending order.

Find the middle value or the average of the two middle values.

Arrange the marks: 0, 20, 40, 60, 80, 100, 120

Total number of students: 80, 76, 50, 28, 18, 9, 3

There's a total of 80 + 76 + 50 + 28 + 18 + 9 + 3 = 264 students.

The median falls between the 132nd and 133rd values (since 264/2 = 132). These correspond to the 20 marks.

So, the median is = 20.

Mode:

The mode is the value that appears most frequently in the data.

The mode is the mark with the highest frequency, i.e., the mark with the highest number of students.

The mode is 0 since it has the highest frequency of 80 students.