Question

Find the sine of ZA.

Simplify your answer and write it as a proper fraction, improper fraction, or whole number.
sin (A) = =

Answer 1

sinA =
`(35)/(37)`

Explanation:

Before obtaining the sinA , we require to calculate the length of the hypotenuse AB

using Pythagoras' identity in the right triangle

AB² = AC² + BC² = 24² + 70² = 576 + 4900 = 5476

take square root of both sides

`√(AB^2)` =
`√(5476)`

AB = 74

Then

sinA =
`(opposite)/(hypotenuse)` =
`(BC)/(AB)` =
`(70)/(74)` =
`(35)/(37)` ( in simplest form )

Answer 2

`\sin(\angle A)=(35)/(37)`

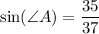
Explanation:

recall that sine is the ratio of the opposite side (to the angle) and the hypotenuse (longest side).

since this is a right triangle, we can use Pythagoras theorem to find the hypotenuse here. recall
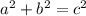`a^2+b^2=c^2` where a, b and c are side lengths and c is the hypotenuse.

thus, we have
`24^2+70^2=5476=c^2`

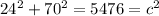
then taking the square root of both sides, we have
`c=74`.

so, we have to take the ratio of the opposite side to
`\angle A`, and the hypotenuse.

the opposite side is 70.

so,
`\sin(\angle A)=(70)/(74)`. dividing both sides by 2, we have

`\sin(\angle A)=(35)/(37)`. thus, we have reached our solution.