Question

Write an equation of a quadratic function that has x-intercepts -1 and -9 and a range of y <= 3

​

Answer 1

`f(x)=-(3)/(16)(x+1)(x+9)=-(3)/(16)(x^2+10x+9)=-(3x^2)/(16)-(15x)/(8)-(27)/(16)`

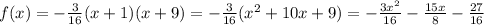
Explanation:

we are to find a quadratic function. first, the two x-intercepts means the roots or solutions of the function are -1 and -9.

so, we can start with letting the function be
`f(x)=k(x+9)(x+1)`. this is because if we let x= -9, f(x) will be equal to 0, which is what we want. also, we let k be a nonzero constant, which will be important for the second point: the range is less than or equal to 3. so, we want to find k such that the maximum value of f(x) is
`\leq 3`.

first, expand the quadratic:
`f(x)=k(x^2+10x+9).` next, we can find the value of x through calculus or finding the vertex of the function. ill assume you need to use the vertex form, so we will complete the square.

`\to f(x)=k[(x+5)^2-25+9)]=k[(x+5)^2-16]`. this is from the completing the square method. so, expanding further gives
`f(x)=k(x+5)^2-16k`. using the vertex formula, we have the vertex coordinates as
`(-5,-16k)`.

so, we need a k such that the y-coordinate becomes 3. so,

`-16k=3\to k=-(3)/(16)`. a negative k is necessary too since we want the parabola to slope downwards.

thus, we have our quadratic as
`f(x)=-(3)/(16)(x^2+10x+9)=-(3x^2)/(16)-(15x)/(8)-(27)/(16)`.

OPTIONAL
the completing the square method:

given a quadratic
`x^2+ax+b=0,` we can find the vertex form by using the fact that
`(x+(a)/(2))^2=x^2+ax+(a^2)/(4)` then using that to find the vertex form. so, we have
`(x+(a)/(2))^2-(a^2)/(4)+b=0` as our vertex form. note that
`b-(a^2)/(4)` is our critical point here.