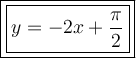Question

Find the equation of the tangent to the curve y=cos^2 x-sin^2 x at the point where x=pi/4

Answer 1

`y=-2x+(\pi)/(2)`

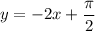
Explanation:

To find the equation of the tangent line of the curve y = cos²x - sin²x at the point where x = π/4, we first need to find the slope (gradient) of the tangent line at this point.

To find the slope of the tangent line at a specific value of x, we need to evaluate the derivative of the function at that particular value of x.

To differentiate y = cos²x - sin²x, first rewrite the function in terms of cos only by using the cosine double angle identities.

`\boxed{\begin{array}{l}\underline{\textsf{Cosine Double Angle Identities}}\\\\\cos 2x=\cos^2 x- \sin^2 x\\\\\cos2x=2 \cos^2 x- 1\\\\\cos 2x=1 - 2 \sin^2 x\\\end{array}}`

Therefore, y = cos²x - sin²x can be rewritten as:

`y=\cos(2x)`

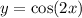
To differentiate y = cos(2x), we can use the chain rule.

`\boxed{\begin{array}{c}\underline{\text{Chain Rule for Differentiation}}\\\\\text{If\;\;$y=f(u)$\;\;and\;\;$u=g(x)$\;\;then:}\\\\\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}*\frac{\text{d}u}{\text{d}x}\end{array}}`

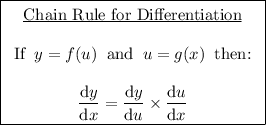
In this case:

`\textsf{Let}\;\;y=\cos(u)\;\;\textsf{where}\;\;u=2x`

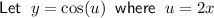
Differentiate the two parts separately:

`y=\cos(u)\implies \frac{\text{d}y}{\text{d}u}=-\sin(u)`

`u=2x\implies \frac{\text{d}u}{\text{d}x}=2`

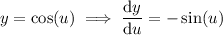
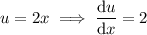
Now, put everything back into the chain rule formula:

`\frac{\text{d}y}{\text{d}x}=-\sin(u) *2`

`\frac{\text{d}y}{\text{d}x}=-2\sin(u)`

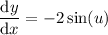
Substitute back in u = 2x:

`\frac{\text{d}y}{\text{d}x}=-2\sin(2x)`

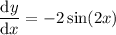
To find the slope of the tangent line at the point where x = π/4, substitute x = π/4 into dy/dx:

`\frac{\text{d}y}{\text{d}x}=-2\sin\left(2\cdot (\pi)/(4)\right)`

`\frac{\text{d}y}{\text{d}x}=-2\sin\left((\pi)/(2)\right)`

`\frac{\text{d}y}{\text{d}x}=-2(1)`

`\frac{\text{d}y}{\text{d}x}=-2`

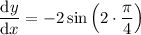
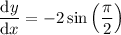
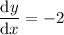
Therefore, the slope of the tangent line is m = -2.

Find the corresponding y-coordinate of the point where x = π/4 by substituting x = π/4 into the equation for y:

`y=\cos\left(2\cdot (\pi)/(4)\right)`

`y=\cos\left((\pi)/(2)\right)`

`y=0`

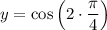
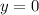
Now, substitute the found slope m = -2 and point (π/4, 0) into the point-slope formula:

`\begin{aligned}y-y_1&=m(x-x_1)\\\\y-0&=-2\left(x-(\pi)/(4)\right)\\\\y&=-2x+(\pi)/(2)\end{aligned}`

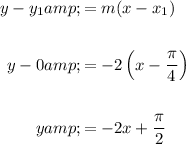
Therefore, the equation of the tangent line of the curve y = cos²x - sin²x at the point where x = π/4 is:

`\large\boxed{\boxed{y=-2x+(\pi)/(2)}}`