Question

Here are three calculus questions..! Attached below are the pictures for them! I greatly thank you for your time.

Answer 1

Explanation:

x^1/2 + y^1/2 = 7

Differentiating:

1/2 x^-1/2 + 1/2 y^-1/2 * y'= 0

y' = -1/2 x^-1/2 / 1/2 y^-1/2

= -x^1/2 / y^-1/2

When x = 25 and y = 4 we have

The slope

= -(25)^-1/2 / (4)^-1/2

= - 1/5 / 1/2

= -2/5.

Answer 2

`\textsf{1)}\quad y'(25)=-(2)/(5)`

`\textsf{2a)}\quad \frac{\text{d}y}{\text{d}x}=- (3y)/(x)`

`\textsf{2b)}\quad \frac{\text{d}y}{\text{d}x}=-0.5926\; \sf (4\;d.p.)`

`\textsf{3)}\quad \textsf{Slope}=-0.323\; \sf (3\;d.p.)`

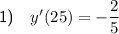
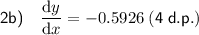
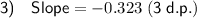
Explanation:

Question 1

`√(x)+√(y)=7`

`y(25)=4`

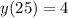
To find y'(25), begin by differentiating √x + √y = 7 using implicit differentiation.

Place d/dx in front of each term of the equation:

`\frac{\text{d}}{\text{d}x}√(x)+\frac{\text{d}}{\text{d}x}√(y)=\frac{\text{d}}{\text{d}x}7`

`\frac{\text{d}}{\text{d}x}x^(\frac12)+\frac{\text{d}}{\text{d}x}y^(\frac12)=\frac{\text{d}}{\text{d}x}7`

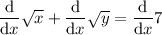
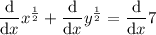
Differentiate the terms in x only (and the constant term):

`(1)/(2)x^(-\frac12)+\frac{\text{d}}{\text{d}x}y^(\frac12)=0`

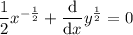
Use the chain rule to differentiate terms in y.

In practice, this means differentiate with respect to y, and place dy/dx at the end:

`\frac12x^(-\frac12)+\frac12y^(-\frac12)(dy)/(dx)=0`

`(1)/(2√(x))+(1)/(2√(y))(dy)/(dx)=0`

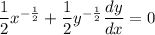
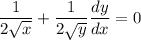
Rearrange to isolate dy/dx:

`(1)/(2√(y))(dy)/(dx)=-(1)/(2√(x))`

`(dy)/(dx)=-(2√(y))/(2√(x))`

`(dy)/(dx)=-(√(y))/(√(x))`

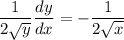
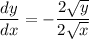
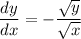
The expression y'(25) means the value of dy/dx when x = 25.

Given that y = 4 when x = 25, substitute these values into the equation for dy/dx to find y'(25):

`y'(25)=-(√(4))/(√(25))`

`y'(25)=-(2)/(5)`

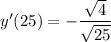
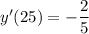
Therefore, the value of y'(25) is -2/5.

`\hrulefill`

Question 2

`100x^(\frac34)y^(\frac14)=5400`

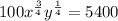
To find dy/dx, begin by placing d/dx in front of each term of the equation:

`\frac{\text{d}}{\text{d}x}100x^(\frac34)y^(\frac14)=\frac{\text{d}}{\text{d}x}5400`

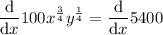
Differentiate the constant:

`\frac{\text{d}}{\text{d}x}100x^{(3)/(4)}y^{(1)/(4)}=0`

Differentiate the left side of the equation using the product rule.

`\boxed{\begin{array}{l}\underline{\sf Product\;Rule\;for\;Differentiation}\\\\\textsf{If}\;y=uv\;\textsf{then:}\\\\\frac{\text{d}y}{\text{d}x}=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}\end{array}}`

`\begin{aligned}\textsf{Let}\;\;u=100x^(\frac34) \implies \frac{\text{d}u}{\text{d}x}&=(3)/(4) \cdot 100x^(\frac34-1)\\\\\frac{\text{d}u}{\text{d}x}&=75x^(-\frac14)\\\\\frac{\text{d}u}{\text{d}x}&=(75)/(x^(\frac14))\end{aligned}`

`\begin{aligned}\textsf{Let}\;\;v=y^(\frac14) \implies \frac{\text{d}v}{\text{d}x}&=(1)/(4) \cdot y^(\frac14-1)\frac{\text{d}y}{\text{d}x}\\\\\frac{\text{d}v}{\text{d}x}&=(1)/(4) y^(-\frac34)\frac{\text{d}y}{\text{d}x}\\\\\frac{\text{d}v}{\text{d}x}&=(1)/(4y^(\frac34)) \frac{\text{d}y}{\text{d}x}\end{aligned}`

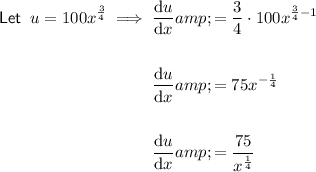
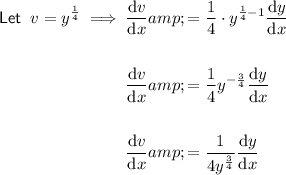
Therefore:

`\begin{aligned}\frac{\text{d}}{\text{d}x}100x^(\frac34)y^(\frac14)&=100x^(\frac34)\cdot(1)/(4y^(\frac34))\frac{\text{d}y}{\text{d}x}+y^(\frac14)\cdot(75)/(x^(\frac14))\\\\&=(25x^(\frac34))/(y^(\frac34))\frac{\text{d}y}{\text{d}x}+(75y^(\frac14))/(x^(\frac14))\end{aligned}`

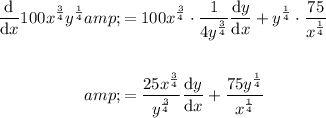
Rearrange the differentiated equation to isolate dy/dx:

`(25x^(\frac34))/(y^(\frac34)) (dy)/(dx)=-(75y^(\frac14))/(x^(\frac14))`

`(dy)/(dx)=- (75y^(\frac14)y^(\frac34))/(25x^(\frac14)x^(\frac34))`

`(dy)/(dx)=- (75y)/(25x)`

`(dy)/(dx)=- (3y)/(x)`

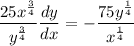
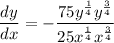
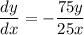
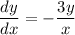
To find the value of dy/dx at point (81, 16), substitute x = 81 and y = 16 into dy/dx:

`(dy)/(dx)=-(3(16))/(81)=-(48)/(81)=-0.5926\;\sf (4\;d.p.)`

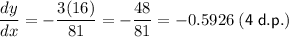
Therefore, the value of dy/dx at the point (81, 16) is -0.5926, rounded to 4 decimal places.

`\hrulefill`

Question 3

`(x^2)/(16)+(y^2)/(25)=1`

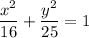
To find the formula for the slope of the tangent line at point (x, y) on the ellipse, differentiate the equation of the ellipse using implicit differentiation.

Begin by placing d/dx in front of each term of the equation:

`\frac{\text{d}}{\text{d}x}(x^2)/(16)+\frac{\text{d}}{\text{d}x}(y^2)/(25)=\frac{\text{d}}{\text{d}x}1`

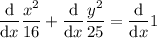
Differentiate the terms in x only (and the constant term):

`2\cdot (x^(2-1))/(16)+\frac{\text{d}}{\text{d}x}(y^2)/(25)=0`

`(x)/(8)+\frac{\text{d}}{\text{d}x}(y^2)/(25)=0`

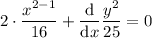
Use the chain rule to differentiate terms in y.

In practice, this means differentiate with respect to y, and place dy/dx at the end:

`(x)/(8)+(2y)/(25)\frac{\text{d}y}{\text{d}x}=0`

Rearrange to isolate dy/dx:

`(2y)/(25)\frac{\text{d}y}{\text{d}x}=-(x)/(8)`

`\frac{\text{d}y}{\text{d}x}=-(25x)/(16y)`

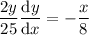
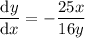
To find the slope of the tangent line at point (1, 4.84), substitute x = 1 and y = 4.84 into dy/dx:

`\frac{\text{d}y}{\text{d}x}=-(25(1))/(16(4.84))=-0.323\; \sf (3\;d.p.)`

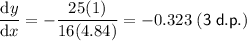
Therefore, the slope of the tangent line is -0.323, rounded to 3 decimal places.