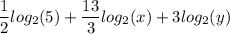Question

Log_2⁡〖(√5x^5 y^3)/(∛x^2 )

Answer 1

The simplified expression to the logarithm expression given is
`(1)/(2)log_2(5) + (13)/(3)log_2(x) + 3 log_2(y)`

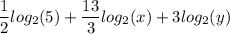
Logarithms expressions and properties.

The simplification of logarithm expression requires the use of different logarithmic approach such as combination of powers and square roots to simplify the expression into simpler forms.

Given that:

`log_2 \Big ( \frac{√(5)x^5y^3}{\sqrt[3]{x^2} } \Big)`

The first step in solving this logarithm expression is to change the form of the denominator to its power.

`log_2 \Big ( (√(5)x^5y^3)/(x^(2/3)) } \Big)`

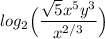
Now, we can combine the square root and the cube root using the law of indices.

`log_2 \Big ( (√(5)x^(5-2/3)y^3)/(1) } \Big)`

`log_2 \Big ( {√(5)x^(13/3)y^3} } \Big)`

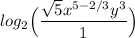
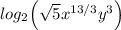
Using Logarithm Properties:
`log_a(bc) = log_a(b) + log_a(c)`, we have:

`log_2 √(5) +log_2(x^(13/3))+log_2(y^3)`

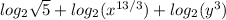
By solving the exponents using the logarithm multiplicative property, we have:

`(1)/(2)log_2(5) + (13)/(3)log_2(x) + 3 log_2(y)`