Answer:
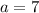
Explanation:
Let's expand the right side of the equation
 and then set it equal to
and then set it equal to
 .
.
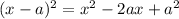
Now, set it equal to
 :
:
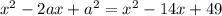
Now, compare the coefficients of corresponding terms:
1. Coefficient of
 :
:
 (no change)
(no change)
2. Coefficient of
 :
:
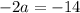
Now, solve for
 :
:
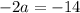
Divide both sides by -2:
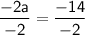
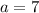
So, the value of
 in the equation
in the equation
 is
is
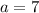 .
.