Answer:
Axis of symmetry:
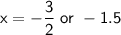
Explanation:
The axis of symmetry for a quadratic function in the form
 can be found using the formula:
can be found using the formula:

For the given quadratic function
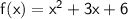 , the coefficients are
, the coefficients are
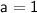 ,
,
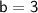 , and
, and
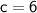 .
.
Now, Substitute these values into the formula:

Simplify the expression:

So, the axis of symmetry for the quadratic function
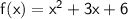 is
is
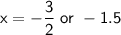 .
.