Question

Integrate (x ^ 2 + 9x + 1)/((x ^ 2 + 1) ^ 2) dx​

Answer 1

`\displaystyle \int (x^2+9x+1)/((x^2+1)^2)\; \text{d}x=\arctan(x)-(9)/(2(x^2+1))+C`

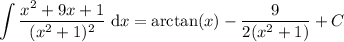
Explanation:

Given integral:

`\displaystyle \int (x^2+9x+1)/((x^2+1)^2)\; \text{d}x`

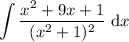
To evaluate the given integral, begin by rewriting the integrand as partial fractions.

As the denominator has a repeated irreducible quadratic factor, and the degree of the denominator is greater than the degree of the numerator, the partial fraction form is:

`\boxed{(N(x))/((x^2+c)^2) \equiv(Ax+B)/((x^2+c))+(Cx+D)/((x^2+c)^2)}`

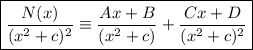
Therefore, the integrand can be written as partial fractions in the form:

`(x^2+9x+1)/((x^2+1)^2)\equiv (Ax+B)/((x^2+1))+(Cx+D)/((x^2+1)^2)`

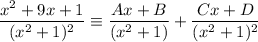
Add the partial fractions:

`(x^2+9x+1)/((x^2+1)^2)\equiv ((Ax+B)(x^2+1)+Cx+D)/((x^2+1)^2)`

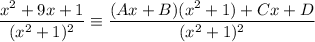
Cancel the denominators from both sides of the original identity, so the numerators are equal:

`x^2+9x+1}=(Ax+B)(x^2+1)+Cx+D`

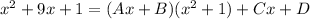
Expand the right side of the equation:

`x^2+9x+1}=Ax^3+Ax+Bx^2+B+Cx+D`

`x^2+9x+1}=Ax^3+Bx^2+(A+C)x+(B+D)`

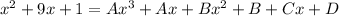
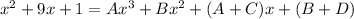
Equate the coefficients:

`A=0`

`B=1`

`A+C=9 \implies 0+C=9 \implies C=9`

`B+D=1 \implies 1+D=1 \implies D=0`

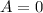
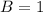
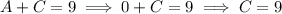
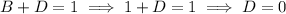
Replace A, B, C and D in the original identity:

`(x^2+9x+1)/((x^2+1)^2)\equiv (1)/((x^2+1))+(9x)/((x^2+1)^2)`

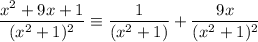
Therefore, the original integral can be written as:

`\displaystyle \int (x^2+9x+1)/((x^2+1)^2)\; \text{d}x=\int (1)/((x^2+1))+(9x)/((x^2+1)^2)\; \text{d}x`

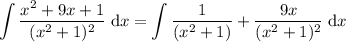
Now that we have decomposed the original rational function into two simpler fractions, we can evaluate the integral by first applying the sum rule, and then using the arctan integration rule:

`\boxed{\displaystyle \int (1)/(x^2+1)\; \text{d}u=\arctan x + \text{C}}`

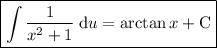
Therefore:

`\begin{aligned}\displaystyle \int (x^2+9x+1)/((x^2+1)^2)\; \text{d}x&=\int (1)/((x^2+1))+(9x)/((x^2+1)^2)\; \text{d}x\\\\&=\int (1)/((x^2+1))\; \text{d}x+\int(9x)/((x^2+1)^2)\; \text{d}x\\\\&=\arctan(x)+\int(9x)/((x^2+1)^2)\; \text{d}x\end{aligned}`

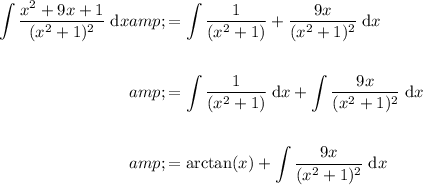
Now, use the method of substitution to evaluate the second integral.

`\begin{aligned}\textsf{Let}\;u &= x^2 + 1 \\\\\textsf{So}\;\;\frac{\text{d}u}{\text{d}x}&=2x \implies \text{d}x=(1)/(2x)\;\text{d}u\end{aligned}`

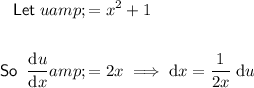
Therefore:

`\begin{aligned}\displaystyle &=\arctan(x)+\int(9x)/(u^2)\cdot (1)/(2x)\;\text{d}u\\\\&=\arctan(x)+\int(9)/(2u^2)\;\text{d}u\\\\&=\arctan(x)+(9)/(2)\int u^(-2)\;\text{d}u\\\\&=\arctan(x)-(9)/(2)u^(-1)+C\\\\&=\arctan(x)-(9)/(2u)+C\\\\&=\arctan(x)-(9)/(2(x^2+1))+C\end{aligned}`

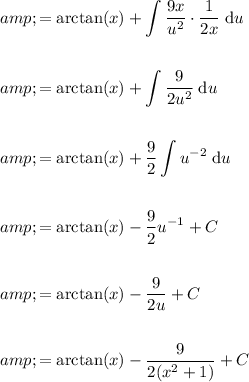
So, the evaluation of the given integral is:

`\boxed{\boxed{\displaystyle \int (x^2+9x+1)/((x^2+1)^2)\; \text{d}x=\arctan(x)-(9)/(2(x^2+1))+C}}`