Question

what is the x-coordinate of the point where the 45-45-90 triangle in this image intersects the unit circle?

Answer 1

The x-coordinate of the point where the 45-45-90 triangle intersects the unit circle is
`\( (√(2))/(2) \)`.

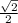In a 45-45-90 triangle inscribed in a unit circle, the hypotenuse is the radius of the circle, which is 1 unit in length. Since this is a right triangle with two angles of 45 degrees, it is an isosceles right triangle, meaning the two legs are of equal length.

Let's denote the length of each leg as
`\( L \)`. By the Pythagorean theorem, we have:

`\[ L^2 + L^2 = 1^2 \]`

`\[ 2L^2 = 1 \]`

`\[ L^2 = (1)/(2) \]`

`\[ L = \sqrt{(1)/(2)} \]`

`\[ L = (√(2))/(2) \]`

Since the unit circle's equation is
`\( x^2 + y^2 = 1 \)`, and we know that the legs of the 45-45-90 triangle are equal, the x-coordinate (as well as the y-coordinate) of the point where the triangle intersects the unit circle at the first quadrant will be
`\( (√(2))/(2) \)`.

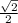Therefore, the x-coordinate of the point where the 45-45-90 triangle intersects the unit circle is
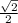`\( (√(2))/(2) \)`.