Question

how many friends must you have in order to guarentee that at least 2 of them have birthdays in the same month? 2

Answer 1

To guarantee that at least two friends have birthdays in the same month, you would need a minimum of 13 friends.

Step-by-step explanation:

The solution involves the application of the Birthday Paradox, a phenomenon where the probability of two people sharing the same birthday is higher than expected. To calculate the minimum number of friends needed for this guarantee, we utilize the complement probability. The probability that no one shares a birthday is given by
`\(\left((11)/(12)\right)^(n-1)\)`, where
`\(n\)` is the number of people. Setting this probability less than 0.5 and solving for
`\(n\)` provides the minimum number of friends required:

`\[ \left((11)/(12)\right)^(n-1) < 0.5 \]`

Solving this inequality yields
`\(n \geq 13\)`, indicating that with 13 friends, there is a greater than 50% chance that at least two of them share the same birth month.

To further illustrate, consider the calculation for
`\(n = 12\):`

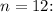
`\[ \left((11)/(12)\right)^(12-1) = \left((11)/(12)\right)^(11) \approx 0.498 \]`

This probability is just below 0.5, and with
`\(n = 13\)`, the probability increases above 0.5:

`\[ \left((11)/(12)\right)^(13-1) = \left((11)/(12)\right)^(12) \approx 0.507 \]`

Hence, having 13 friends ensures a greater than 50% likelihood of at least two friends sharing the same birth month, showcasing the intriguing aspects of probability in the context of the Birthday Paradox.