Answer:
 yards
yards
 yards
yards
Explanation:
Let's denote the width of the rectangle as
 and the length as
and the length as
 . According to the given information:
. According to the given information:
1. The length is 9 more than the width:
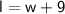 .
.
2. The area of the rectangle is 112 square yards:
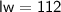 .
.
Now, we can set up a system of equations using the above information:
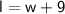
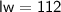
Substitute the expression for
 from the first equation into the second equation:
from the first equation into the second equation:
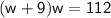
Expand and rearrange the equation:

Now, factor the quadratic equation:
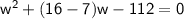
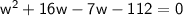
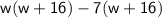
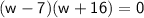
This gives two possible solutions for
 :
:
1.
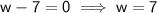
2.
 (discarded as width cannot be negative)
(discarded as width cannot be negative)
So, the width of the rectangle is
 . Now, substitute this value back into the expression for
. Now, substitute this value back into the expression for
 :
:
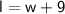
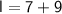
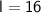
Therefore, the length of the rectangle is
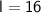 yards, and the width is
yards, and the width is
 yards.
yards.