Question

PLEASE HELP ME!!

1) determine the coordinate of B

2) Determine the coordinate of C

3) describe the transformation from ABC TO A’ B’ C’

4) write an algebraic rule for the transformation from ABC to A’ B’ C’

5) if P is reflected about the line y = x, determine the new coordinate

6) write an algebraic rule for the reflection about the line y = x for any coordinate

Answer 1

1) B(6, 2)

2) C(1, 2)

3) Translation of 6 units left and 7 units down.

4) (x, y) → (x - 6, y - 7)

5) P' = (-2, 4)

6) (x, y) → (y, x)

Explanation:

Question 1

ABC is a right triangle with vertices A(6, 7), B(m, n) and C(1, 2). AB is a vertical line and BC is a horizontal line. Therefore, the x-coordinate of B is the same as the x-coordinate of A, and the y-coordinate of B is the same is the y-coordinate of C. So, the coordinates of point B are (6, 2).

Question 2

From observation of the graph, we can see that the coordinates of C are (1, 2).

Question 3

To determine the transformation that maps triangle ABC to triangle A'B'C', we can examine the coordinates of points A and A'. Point A is located at (6, 7), and point A' is located at the origin (0, 0). Therefore, for point A to be transformed to point A', we need to translate the point 6 units left and 7 units down.

Question 4

Translating a point 6 units left means subtracting 6 units from its x-coordinate. Translating a point 7 units down means subtracting 7 units from its y-coordinate. Therefore, the mapping rule that transforms ABC to A'B'C' is:

`(x,y) \rightarrow (x-6, y-7)`

Question 5

The location of point P is (4, -2). If it is reflected about the line y = x, the new coordinates can be found by swapping the x and y coordinates. Therefore, the reflection of point P across the line y = x is given by the coordinates P' = (-2, 4).

Question 6

The algebraic rule for a reflection about the line y = x can be expressed as:

`(x, y) \rightarrow (y, x)`

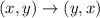
This rule states that the reflected point is obtained by swapping the x- and y-coordinates of the original point.