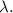Final answer:
The de Broglie wavelength of a nitrogen molecule can be determined using its rms velocity and the de Broglie relation, which involves Planck's constant and the particle's momentum.
Step-by-step explanation:
The de Broglie wavelength
 of a particle is given by the de Broglie wavelength formula:
of a particle is given by the de Broglie wavelength formula:
![\[\lambda = (h)/(p)\]](https://img.qammunity.org/2024/formulas/biology/high-school/gncbb9oas65hhbphbsgi9k480yugqv1dku.png)
where:
 is the de Broglie wavelength,
is the de Broglie wavelength,
 is Planck's constant
is Planck's constant
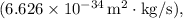
 is the momentum of the particle.
is the momentum of the particle.
The momentum
 of a particle is given by:
of a particle is given by:
![\[p = m \cdot v\]](https://img.qammunity.org/2024/formulas/biology/high-school/j16ff1ymn1qhsnmpoyzqcslsd8zpqfqsac.png)
where:
 is the mass of the particle,
is the mass of the particle,
 is the velocity of the particle.
is the velocity of the particle.
For a nitrogen molecule
 , the mass
, the mass
 is the total mass of the molecule. The root mean square velocity
is the total mass of the molecule. The root mean square velocity
 is related to the velocity of the particles in a gas, and it is given by:
is related to the velocity of the particles in a gas, and it is given by:
![\[v_{\text{rms}} = \sqrt{(3 \cdot k \cdot T)/(m)}\]](https://img.qammunity.org/2024/formulas/biology/high-school/ctfp2amgk3qo80wdlytom2vpkv3zv3uppf.png)
where:
 is the Boltzmann constant
is the Boltzmann constant

 is the temperature in kelvin.
is the temperature in kelvin.
Let's calculate it for nitrogen
 at a temperature of 400 K.
at a temperature of 400 K.
First, we find
 :
:
![\[v_{\text{rms}} = \sqrt{(3 \cdot k \cdot T)/(m)}\]](https://img.qammunity.org/2024/formulas/biology/high-school/ctfp2amgk3qo80wdlytom2vpkv3zv3uppf.png)
Substitute the values:
![\[v_{\text{rms}} = \sqrt{\frac{3 \cdot (1.381 * 10^(-23) \, \text{J/K}) \cdot 400 \, \text{K}}{m_(N_2)}}\]](https://img.qammunity.org/2024/formulas/biology/high-school/tax5lv1jva1xciyd4swp5nfx6mylhchyq4.png)
The molar mass of
 is approximately
is approximately
 , so the mass of one nitrogen molecule
, so the mass of one nitrogen molecule
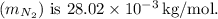
Now, calculate
 , and then use it to find the momentum
, and then use it to find the momentum
 and finally the de Broglie wavelength
and finally the de Broglie wavelength