Question

if young's modulus of the material is three times of its modulus of rigidity, then its volume elasticity will be

Answer 1

The volume elasticity of the material will be (4/3) times the Young's modulus.

Step-by-step explanation:

The relationship between Young's modulus (Y), modulus of rigidity (G), and volume elasticity (K) in isotropic materials is given by the equation
`\(K = (Y)/(3(1-2\\u))\),` where
`\(\\u\)` is Poisson's ratio. When the Young's modulus is three times the modulus of rigidity, we can establish a ratio: (Y = 3G). To find (K), we use the relationship
`\(K = (Y)/(3(1-2\\u))\)` and substitute (Y = 3G):

`\(K = (3G)/(3(1-2\\u))\)`

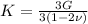
Simplifying,
`\(K = (G)/(1-2\\u)\).`

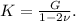
For isotropic materials, Poisson's ratio
`(\(\\u\))` typically equals (0.25). Substituting this value into the equation:

`\(K = (G)/(1-2(0.25)) = (G)/(0.5) = 2G\)`

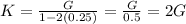
This implies that the volume elasticity \(K\) is twice the modulus of rigidity (G).

Therefore, when the Young's modulus is three times the modulus of rigidity, the volume elasticity of the material will be (4/3) times the Young's modulus.