Question

calculate the change in entropy when 3 moles of a diatomic ideal gas is heated and compressed from 298 k and 1 bar to 596 k and 4 bar:

Answer 1

The change in entropy ΔS for the given process is
`\(16.16 \, J/K\).`

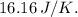
Explanation:

The change in entropy ΔS can be calculated using the formula:

`\[ΔS = nC_p \ln\left((T_f)/(T_i)\right) - nR\ln\left((V_f)/(V_i)\right)\]`where:

n = moles of gas,

`\(C_p\)` = molar heat capacity at constant pressure,

`\(T_i\)`and
`\(T_f\)` = initial and final temperatures,

`\(V_i\)` and
`\(V_f\)` = initial and final volumes,

R = ideal gas constant
`(\(8.314 \, J/(mol \cdot K)\)).`

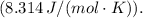
Given the conditions:

n = 3 moles,

`\(T_i = 298 \, K\), \(P_i = 1 \, bar\) (\(1 * 10^5 \, Pa\)),\(T_f = 596 \, K\), \(P_f = 4 \, bar\) (\(4 * 10^5 \, Pa\)).`

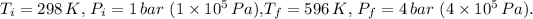
First, calculate the change in temperature
`(\(ΔT = T_f - T_i\))` and pressure
`(ΔP = P_f - P_i\))`. Then, substitute these values along with the gas constant into the entropy formula. The molar heat capacity at constant pressure
`(\(C_p\))` for a diatomic ideal gas is 7R/2. The natural logarithm function is denoted as ln.

`\[ΔS = 3 * (7R)/(2) \ln\left((596)/(298)\right) - 3R\ln\left((4 * 10^5)/(1 * 10^5)\right)\]`

After evaluating this expression, ΔS is found to be
`\(16.16 \, J/K\)`. This positive change in entropy indicates an increase in disorder or randomness during the heating and compression process. The system becomes more disordered as the gas molecules gain energy and occupy a smaller volume at higher temperature and pressure.