Question

Help. Me. Please i really need it

Answer 1

4.1) Mean = 106.4

4.2) Median = 122.5

4.3) First quartile = 95

4.4) Third quartile = 135

4.5) Interquartile range = 40

Explanation:

To determine the mean, median, first quartile, third quartile and interquartile range of the given data set, we first need to arrange the given data values in ascending order:

12, 60, 95, 105, 120, 125, 130, 135, 140, 142

Mean

The mean (average) of a data set can be calculated by dividing the sum of all the data values by the total number of data values:

`\begin{aligned}\textsf{Mean}&=\sf (12+60+95+105+120+125+130+135+140+142)/(10)\\\\&=\sf (1064)/(10)\\\\&=\sf 106.4\end{aligned}`

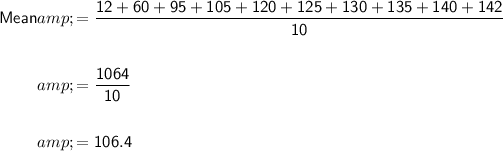
Therefore, the mean of the given data set is 106.4.

Median

The median of a data set is the middle value when the values are arranged in ascending or descending order. Since the given data set has an even number of data values (10), the median is the mean of the middle two values (4th and 5th):

`\textsf{Median}=\sf (120+125)/(2)=(245)/(2)=122.5`

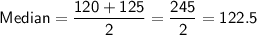
Therefore, the median of the given data set is 122.5.

First and Third Quartiles

The first quartile (Q1) of a data set is the median of the lower half of the data set. As there are 5 data values to the left of the median, the first quartile is middle value of those data values.

The third quartile (Q3) of a data set is the median of the upper half of the data set. As there are 5 data values to the right of the median, the third quartile is middle value of those data values.

`\sf 12, 60, \boxed{\sf 95}, 105, 120\;|\;125, 130, \boxed{\sf 135}, 140, 142\\\phantom{b...)ww}\uparrow\qquad\qquad\;\;\: \uparrow\qquad \qquad\;\;\:\uparrow\\\sf \phantom{ww))w}Q1\qquad\quad Median \qquad\;\;\;\:\: Q3`

Therefore, the first quartile of the given data set is 95, and the third quartile of the given data set is 135.

Interquartile Range (IQR)

The interquartile range (IQR) of a data set is the difference between the third quartile (Q3) and the first quartile (Q1). Therefore:

`\sf IQR=Q3-Q1=135-95=40`

So, the interquartile range of the given data set is 40.

Answer 2

The determination of the following based on the arranged data is as follows:

4.1 Mean = 106.4

4.2 Median = 122.5

4.3 First Quartile = 95

4.4 Third Quartile = 135

4.5 Interquartile range = 40.

How the mean, median, first and third quartiles and interquartile range:

The mean is the average value. The median is the middle value.

The first quartile or the lower quartile is the value under which 25% of data points are found when they are arranged in increasing order.

The third quartile or upper quartile is the value under which 75% of data points are found when arranged in increasing order.

Arranged data:

12, 60, 95, 105, 120, 125, 130, 135, 140, 142

Total value = 1,064 (12 + 60 + 95 + 105 + 120 + 125 + 130 + 135 + 140 + 142)

Number of data items, n = 10

Calculations:

4.1 Mean = 106.4 (1,064 ÷ 10)

4.2 Median = 122.5 {(120 + 125) ÷ 2}

4.3 First Quartile = 1/4(10 + 1) = 2.75th term = 95

4.4 Third Quartile = 3/4(10 + 1) = 8.25th term = 135

4.5 Interquartile range = 40 (135 - 95)