Question

what is the molar solubility (in mol l-1) of a salt with general molecular formula mx (where m is a cation and x is an anion) in a solution already containing 0.486 mol l-1 m ?the ksp of mx

Answer 1

The molar solubility
`(\(s\))` of the salt
`\(MX\)` in a solution containing
`\(0.486 \, \text{mol L}^(-1) \, M\)` is determined by the expression
`\(s^2 = \text{K}_{\text{sp}}/(\text{M} - s)\), where \(\text{K}_{\text{sp}}\)` is the solubility product constant. Solving for
`\(s\)` yields the molar solubility.

Step-by-step explanation:

To find the molar solubility
`(\(s\))` of the salt
`\(MX\)`, we start with the equilibrium expression for the dissolution of the salt:

`\[ MX \rightleftharpoons M^(+)_x + xX^(-) \]`

The equilibrium constant
`(\(K_{\text{sp}}\))` for this reaction is expressed as
`\(K_{\text{sp}} = [M^(+)]^x [X^-]^x\)`. Since the stoichiometry is 1:1 for
`\(MX\), we can simplify this to \(K_{\text{sp}} = s^2\).`

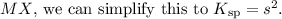
Now, the solution already contains
`\(0.486 \, \text{mol L}^(-1) \, M\),` which contributes to the concentration of
`\(M^(+)\)` ions. Thus, the equilibrium concentration of
`\(M^(+)\) is \(\text{M} - s\)`. Substituting this into the
`\(K_{\text{sp}}\) expression, we get \(s^2 = \text{K}_{\text{sp}}/(\text{M} - s)\).`

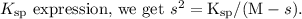
Solving this quadratic equation for
`\(s\),` we obtain the molar solubility. It's important to note that this approach considers the common ion effect from the initial concentration of
`\(M\)`. Understanding these principles is fundamental in predicting the behavior of salts in solution.

Lastly, calculating
`\(s\)` provides insights into the saturation point of the solution, helping to assess potential precipitation or the formation of complexes.

The complete question is:

"What is the molar solubility (in mol L⁻¹) of a salt with the general molecular formula
`\(MX\) (where \(M\)` is a cation and
`\(X\)` is an anion) in a solution that initially contains
`\(0.486 \, \text{mol L}^(-1) \, M\)`? Given the solubility product constant
`(\(K_{\text{sp}}\)) for \(MX\),` determine the equilibrium concentration of
`\(MX\)` in the solution."