Question

Please help me if really appreciate it

Given:
in the diagram PN || ND

1) calculate the value of x

2) calculate the value of y

Answer 1

x = 68 , y = 49

Explanation:

(1)

given PN || ND , then

∠ NCD = ∠ MCQ = 44° ( vertically opposite angles )

the sum of the 3 angles in Δ CND = 180° , that is

x + 68° + 44° = 180°

x + 112° = 180° ( subtract 112° from both sides )

x = 68°

-----------------------------------------------

(2)

y and - 3y + 278 lie on a straight line and are a linear pair , and sum to 180°

y - 3y + 278 = 180

- 2y + 278 = 180 ( subtract 278 from both sides )

- 2y = - 98 ( divide both sides by - 2 )

y = 49

Answer 2

`\sf x = 68^\circ`

`\sf y = 49^\circ`

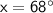
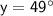
Explanation:

(1)

Given: ∠PN || ∠ND

Then, according to the vertical angle property:

`\sf \angle NCD = \angle MCQ = 44^\circ`

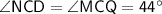
Now, considering the sum of interior angles of a triangle CDN is 180°:

`\sf x + 68^\circ + 44^\circ = 180^\circ`

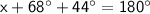
Solving for
`\sf x`:

`\sf x + 112^\circ = 180^\circ`

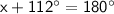
Subtract 112° on both sides:

`\sf x + 112^\circ - 112^\circ = 180^\circ - 112^\circ`

`\sf x = 68^\circ`

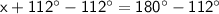
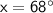
(2)

For the linear pair of angles
`\sf y` and
`\sf -3y + 278`:

And linear pair are supplementary:

`\sf y + (-3y + 278) = 180^\circ`

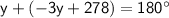
Combine like terms:

`\sf -2y + 278 = 180^\circ`

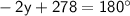
Subtract 278 from both sides:

`\sf -2y + 278 -278= 180^\circ -278`

`\sf -2y = -98`

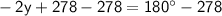
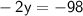
Divide both sides by -2:

`(-2y)/(-2)=(-98)/(-2)`

`\sf y = 49`

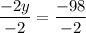
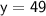
So, the solutions are
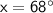`\sf x = 68^\circ` for the first problem and
`\sf y = 49 ^\circ` for the second problem.