Question

The perimeter of a rectangle is 46 cm. If the length = (2x + 5) cm and the breadth= (x + 6) cm, calculate the area of the rectangle. ​

Answer 1

130 cm²

Explanation:

we are given the perimeter of a rectangle to be 46, and the side lengths given as 2x+5 and x+6. we know that

`p = 2(l + b)`

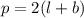
where p is perimeter, l is length and b is breadth. now we plug in values to find the value of x.

`46 = 2(2x + 5 + x + 6)`

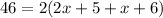
first, we can divide both sides by 2.

`23 = 2x + 5 + x + 6`

then, we will collect like terms.

`2x + x = 23 - 5 - 6`

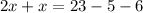
then simplify

`3x = 23 - 11 = 12`

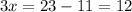
finally, divide both sides by 3.

`\therefore \: x = 4`

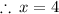
next, we find the dimensions by plugging in x as 4.

2(4) + 5 = 13

4 + 6 = 10

finally, we find the area using the formula:

`a = lb`

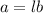
where a is area.

thus, we have

`a = 10 * 13 = 130`

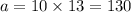
therefore, our area is 130 cm²

Answer 2

`\sf Area = 130 \, \textsf{cm}^2`

Explanation:

The perimeter (P) of a rectangle is given by the formula:

`\sf P = 2 * (\text{length} + \text{breadth})`

In this case, the length (
`\sf L`) is given by
`\sf 2x + 5` and the breadth (
`\sf B`) is given by
`\sf x + 6`. So, the perimeter equation becomes:

`\sf 46 = 2 * ((2x + 5) + (x + 6))`

Now, let's solve for
`\sf x`:

`\sf 46 = 2 * (3x + 11)`

`\sf 23 = 3x + 11`

Subtract 11 from both sides:

`\sf 23 - 11 = 3x + 11 -11`

`\sf 12 = 3x`

Divide by 3:

`\sf (12)/(3) =( 3x)/(3)`

`\sf 4 = x`

`\sf x = 4`

Now that we have found
`\sf x`, we can find the length and breadth:

Length (
`\sf L`) =
`\sf 2x + 5 = 2(4) + 5 = 13` cm

Breadth (
`\sf B`) =
`\sf x + 6 = 4 + 6 = 10` cm

Now, to find the area (
`\sf A`) of the rectangle, use the formula:

`\sf A = \text{length} * \text{breadth}`

`\sf A = 13 * 10`

`\sf A = 130 \, \text{cm}^2`

Therefore, the area of the rectangle is
`\sf 130 \, \textsf{cm}^2`.