Question

How long does it take for light to get from one end of Gomez's Hamburger to the other?

Answer 1

Assuming a standard length of 10 centimeters, light takes approximately 33.3 nanoseconds to travel across Gomez's Hamburger, showcasing the incredible speed of light and the precision of fundamental constants in practical contexts.

Step-by-step explanation:

In contemplating the duration for light to traverse the expanse of Gomez's Hamburger, a foundational formula comes into play:
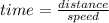`\(time = (distance)/(speed)\)` . With the speed of light in a vacuum standing at roughly
`\(3.00 × 10^8 m/s\),` and envisaging a standard hamburger length of
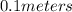`\(0.1 meters\)` , the resulting calculation unfurls a minuscule temporal window of
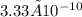`\(3.33 × 10^(-10)\)` seconds, equivalent to
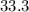`\(33.3\)` nanoseconds.

This fractional timeframe accentuates the extraordinary rapidity inherent in the movement of light. The insignificance of this temporal measure in our day-to-day experiences underscores the astonishing pace at which light traverses space. The constant speed of light becomes a litmus test for the nimbleness with which data and energy can traverse spatial dimensions.

These computations not only underscore the fleeting nature of time in the realm of light but also shed light on the precision and meticulousness with which we can quantify the impact of universal constants, offering a fascinating glimpse into the intricacies of the foundational principles that govern our physical reality.