Question

If
`f(x)=(-3x^2/8)+3x`
find the instantaneous rate of change at (4,6)

Answer 1

0

Explanation:

to find the rate of change of a function at a point we can find the derivative of the function at that point.

first, we shall differentiate the function
`f(x)=(-3x^2)/(8)+3x`.

recall the power rule in differentiation:
`f(x)=x^n\implies f'(x)=nx^(n-1)`.

now let us find the derivative of the function.

`f'(x)=(-3)/(8)(2x)+3=(-3x)/(4)+3` using the power rule and linearity.

next, we have to substitute the value
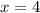`x=4` into the derivative function.

`f'(4)=(-3(4))/(4)+3=-3+3=0`.

so, our rate of change at
`(4,6)` is in fact 0, meaning
`(4,6)` is a stationary point.