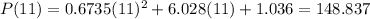Question

Imports of coffee into a country during the years 1999 through 2010 can be modeled by the polynomial function: P(x) = 0.6735x² +6.028x+1.036, where x = 0 represents 1999, x = 1 represents 2000, and so on, and P(x) is in millions of pounds. Use this function to approximate the amount of coffee imported into the country in each given year. (a) 1999 (b) 2005 (c) 2010

Answer 1

a) 1.036

b) 61.45

c) 148.837

Explanation:

we are given the polynomial function
`P(x)=0.6735x^2+6.028x+1.036`, and to find specific values of
`P(x)`, we are to substitute appropriate values of x.

for 1999, we are given that
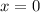`x=0` and so we are to find
`P(0)`.

`P(0)=0.6735(0)^2+6.028(0)+1.036=1.036`

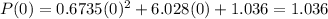
next, for 2005, we are given that
`x=6.`

`P(6)=0.6735(6)^2+6.028(6)+1.036=61.45`

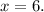
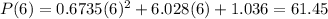
finally, for 2010 we are given that
`x=11`.

`P(11)=0.6735(11)^2+6.028(11)+1.036=148.837`

Answer 2

To answer each part, you would plug in how many years from 1999 there are from the given year. Then multiply each answer by 1,000,000

a) In the problem, it says x=0 represents 1999, so we would plug in 0 for x, getting 1.036. Now we would multiply this answer by 1 million to get 1,036,000 pounds of coffee

b) In the problem, it says 2005, so we would do 2005-1999, which is equal to 6, so we would plug in 6 for x, getting 60.154. Now we would multiply this answer by 1 million to get 60,154,000 pounds of coffee

c) In the problem, it says 2010, so we would do 2010-1999, which is equal to 11, so we would plug in 11 for x, getting 144.4815. Now we would multiply this answer by 1 million to get 144,481,500 pounds of coffee