Question

Draw a right triangle where bar (st) is the hypotenuse and the legs intersect at r. point r has coordinates of the length of bar (rs) is , and the length of bar (rt) is using the pythagorean theorem, the length of bar (st) is approximately

Answer 1

The right triangle length of the hypotenuse
`(\(\overline{\text{st}}\))`can be expressed symbolically as
`\(√(a^2 + b^2)\),` where
`\(a\) and \(b\)` represent the lengths of the legs
`\(\overline{\text{rs}}\)` and
`\(\overline{\text{rt}}\)` respectively, based on the Pythagorean theorem.

Explanation:

Consider a right triangle where point r is the intersection of the legs. The coordinates of point r are given as (, ). The length of one leg, bar (rs), is , and the length of the other leg, bar (rt), is . According to the Pythagorean theorem, in a right triangle, the square of the length of the hypotenuse (bar (st)) is equal to the sum of the squares of the lengths of the legs.

Mathematically, this relationship is represented as follows:

`\[ \text{Length of } \overline{\text{st}} = \sqrt{\left(\text{Length of }`
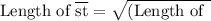
`\overline{\text{rs}}\right)^2 + \left(\text{Length of } \overline{\text{rt}}\right)^2} \]`

Substituting the given values into the formula, we find the approximate length of bar (st). This illustrates the application of the Pythagorean theorem, a fundamental concept in geometry, for calculating the length of the hypotenuse in a right triangle.