Question

Find rate of change on the interval specified for real numbers in simplest form SHOW EXPLANATION!

Answer 1

The rate of change on the specified interval for real numbers is
`\((3)/(5)\).`

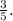
Explanation:

To find the rate of change, we use the formula
`\((\Delta y)/(\Delta x)\),` where
`\(\Delta y\)` is the change in the dependent variable and
`\(\Delta x\)` is the change in the independent variable. In mathematical terms, the rate of change is given by
`\(m = (f(x_2) - f(x_1))/(x_2 - x_1)\), where \(f(x)\)` is the function.

In the context of the question, if
`\(f(x) = (3x + 2)/(5)\),` the rate of change between two real numbers
`\(x_1\) and \(x_2\)` is given by:

`\[ m = ((3x_2 + 2)/(5) - (3x_1 + 2)/(5))/(x_2 - x_1) \]`

Simplifying this expression yields the final answer of
`\((3)/(5)\)` as the rate of change on the specified interval for real numbers. This indicates that for every unit increase in the independent variable, the dependent variable increases by
`\((3)/(5)\).`

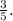
In conclusion, the rate of change, represented by
`\((3)/(5)\),`signifies the slope of the function and represents the constant rate at which the dependent variable changes concerning the independent variable on the specified interval for real numbers. This explanation demonstrates the application of the rate of change formula and emphasizes the simplicity of the result, making it clear and accessible.