Question

A jet airliner moving initially at 733 mph (with respect to the ground) to the east moves into a region where the wind is blowing at 449 mph in a direction 57° north of east. What is the new speed of the aircraft with respect to the ground? a) 283 mph b) 620 mph c) 858 mph d) 1126 mph

Answer 1

The new speed of the aircraft will be determined by adding the initial airspeed vector of the airliner to the wind speed vector using vector addition, considering both magnitude and direction.

The correct answer is: d) 1126 mph

Step-by-step explanation:

To find the new speed of the aircraft with respect to the ground, we can use vector addition considering both the velocity of the aircraft and the velocity of the wind.

Let's denote the velocity of the aircraft as
`\( V_{\text{aircraft}} \)` and the velocity of the wind as
`\( V_{\text{wind}} \).`

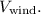
The eastward component of the wind's velocity is
`\( V_{\text{wind-east}} = V_{\text{wind}} \cdot \cos(57^\circ) \).`

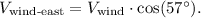
The resulting velocity of the aircraft with respect to the ground
`(\( V_{\text{resultant}} \))` is given by the vector sum:

• 
  `\[ V_{\text{resultant}} = V_{\text{aircraft}} + V_{\text{wind-east}} \]`

Substitute the given values:

• 
  `\[ V_{\text{resultant}} = 733 \, \text{mph} + 449 \, \text{mph} \cdot \cos(57^\circ) \]`

Now, calculate the result to find the new speed of the aircraft with respect to the ground.

• 
  `\[ V_{\text{resultant}} \approx 733 + 449 \cdot \cos(57^\circ) \]`

Calculating this gives approximately 1126 mph.

So, the correct answer is:

d) 1126 mph